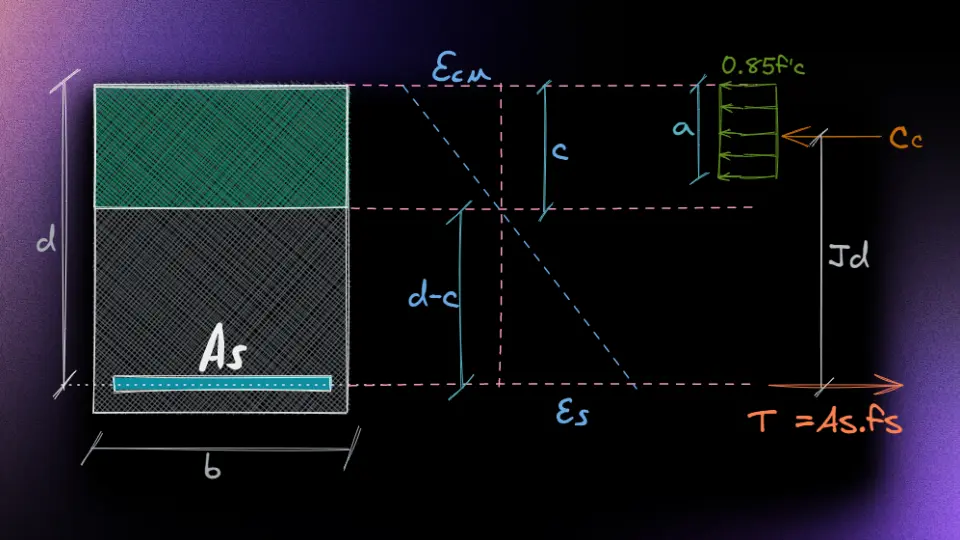
Flexión Simple

1. Tipos de falla

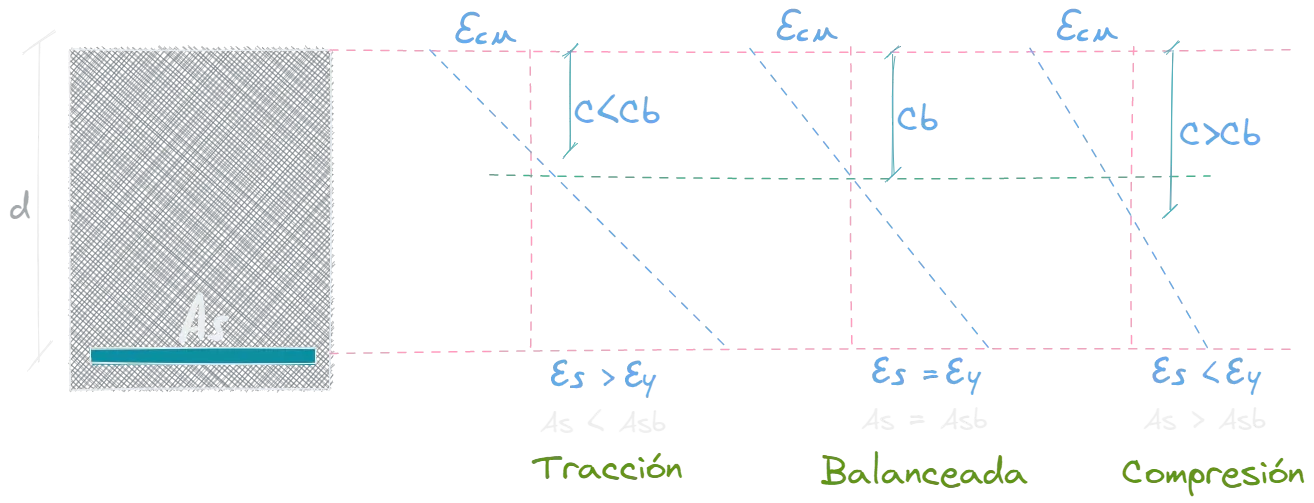
1.1. Falla en tracción (sub reforzada)

Este tipo de falla es la que se quiere conseguir siempre cuando se diseña. Esto se debe a que la falla a tracción es dúctil y con capacidad de disipar energía. Como se observa en la imagen, esto se logra cuando la deformación unitaria del acero es mayor a la deformación unitaria del acero en fluencia.

1.2. Falla balanceada

Este tipo de falla se produce cuando la deformación unitaria del acero alcanza la fluencia en simultaneo con la deformación unitaria de agotamiento del concreto (εcμ). Hallar el acero que produce la falla balanceada es muy importante debido a que las normas delimitan el acero máximo como una fracción de este.

1.3. Falla en compresión (sobre reforzada)

Este tipo de falla se debe evitar debido a que el comportamiento es frágil y con poca capacidad de disipar energía. Esta falla se produce cuando el concreto alcanza su deformación unitaria de agotamiento ($\varepsilon _{c \mu}$) y el acero aún sigue en estado elástico ($\varepsilon _{s} < \varepsilon _{y}$); es decir, aún no llega a la fluencia. Este concepto es muy importante ya que muchas personas pueden pensar que colocar más acero siempre es mejor. A veces, como en el caso de sobre pasar el acero balanceado, se hace un perjuicio a la estructura debido a la falla frágil que puede presentar.

2. Análisis de secciones rectangulares

2.1. Análisis con falla en tracción

En esta falla se está asumiendo que el acero instalado es menor al acero balanceado y que la deformación unitaria del acero es mayor a la deformación unitaria de fluencia del acero. Esto último se deberá corroborar con los cálculos.

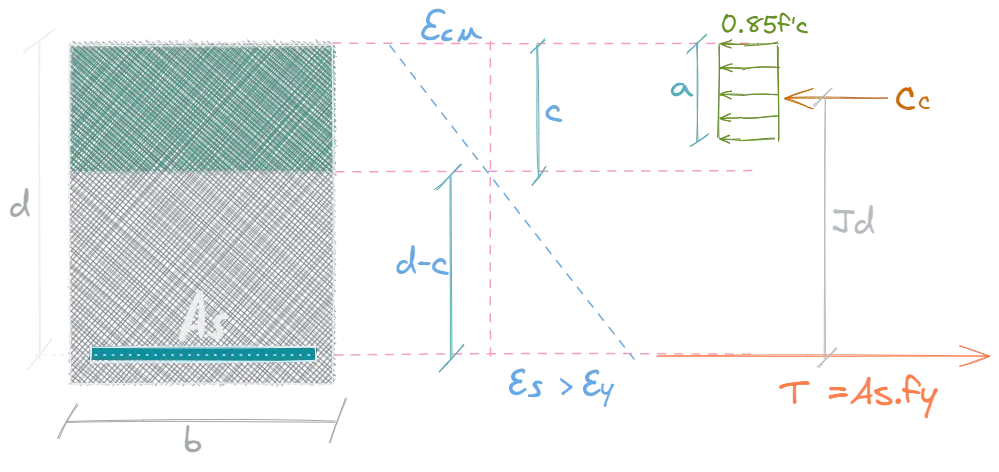
Ecuaciones:

• $a=\beta_1 \cdot c$

• $\begin{cases} \beta _{1} =0.85 & ;f'c\leqslant 280\ kg/cm^{2}\\ \beta _{1} =1.05-\frac{0.714}{1000} f'c\ & ;280\ kg/cm^{2} \leqslant f'c\leqslant \ 560\ kg/cm^{2}\\ \beta _{1} =0.65 & ;f'c\geqslant 560\ kg/cm^{2} \end{cases}$

• $C_c=0.85 \cdot f'c \cdot a \cdot b$

• $T = As \cdot fs = As \cdot fy$

• $a= \frac{As \cdot fy}{0.85 \cdot f'c \cdot b}$

• $Mn = T \cdot (Jd) = As \cdot fy \cdot (d-\frac{a}{2})$

• Verificar: $\varepsilon_s>\varepsilon_y$

2.2. Análisis con falla en compresión

En este tipo de falla la dificultad radica en que no se conoce el esfuerzo del acero en tracción debido a que este no llega a fluir al momento de la falla. La norma peruana E.060 no permite el uso de secciones sobre reforzadas; sin embargo, las ecuaciones para la resistencia de estas secciones se presentan a continuación.

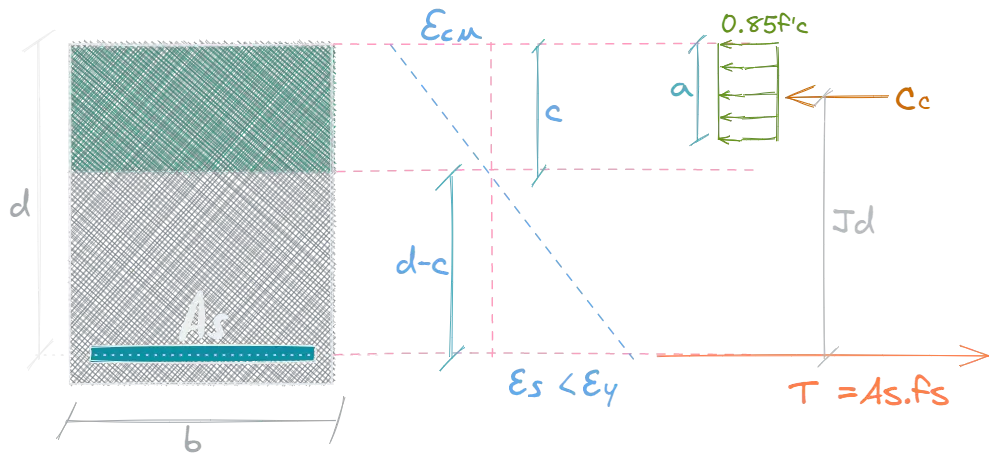
Ecuaciones:

• $C_c=T \Longrightarrow 0.85 \cdot f'c \cdot b \cdot a = As \cdot fs \ \ \ \ (a)$

• $\frac{\varepsilon_s}{\varepsilon_{c\mu}}=\frac{d-c}{c} \Longrightarrow \varepsilon_s=0.003 \cdot \frac{d-c}{c}$

• $fs=\varepsilon_s \cdot E_s = 0.003 \cdot \frac{d-c}{c} = 0.003 \cdot E_s \frac{\beta_1 \cdot d - a}{a} \ \ \ \ (b)$

• $\rho = \frac{As}{b \cdot d} \ \ \ \ (c)$

Sustituyendo $(b)$ y $(c)$ en $(a)$ se obtiene la siguiente ecuación, de la cual se despeja la profundidad del bloque equivalente de compresiones:

$(\frac{0.85 \cdot f'c}{0.003 \cdot E_s \cdot \rho}) \cdot a^2 +a \cdot d - \beta_1 \cdot d^2 = 0$

Finalmente, se tiene la resistencia de la sección:

$Mn = C_c \cdot (Jd) = 0.85 \cdot f'c \cdot a \cdot b \cdot (d-\frac{a}{2})$

Verificar: $\varepsilon_s<\varepsilon_y$

2.3. Análisis con falla balanceada

En este tipo de falla el concreto alcanza la deformación de agotamiento ( $\varepsilon_{c \mu}$) al mismo instante que el acero alcanza la deformación de fluencia ($\varepsilon _{s} = \varepsilon _{y}$).

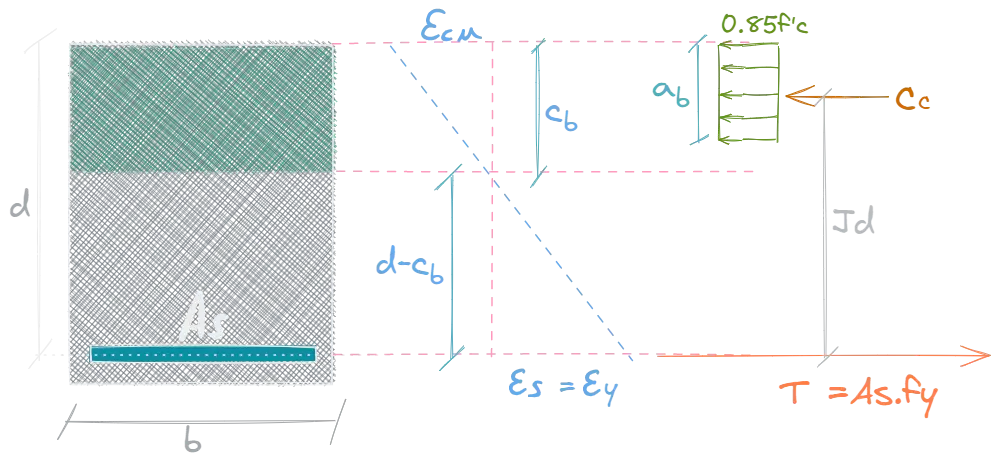
Ecuaciones:

• $\frac{c_b}{d}=\frac{\varepsilon_{c \mu}}{\varepsilon_{c \mu}+\varepsilon_{y}}$

• $C_c = T \Rightarrow 0.85 \cdot f'c \cdot b \cdot a_b = A_s \cdot f_y$

$\ \ \ \ \ \ \ \Longrightarrow A_s = b \cdot [\frac{0.85 \cdot f'c}{f_y} \cdot a_b]$

$\ \ \ \ \ \ \ \Longrightarrow A_s = b \cdot [\frac{0.85 \cdot f'c}{f_y} \cdot \beta _1 \cdot \frac{c_b}{d}]$

$\ \ \ \ \ \ \ \Longrightarrow A_s = b \cdot [\frac{0.85 \cdot f'c}{f_y} \cdot (\frac{\varepsilon_{c \mu}}{\varepsilon_{c \mu}+\varepsilon_{y}})]$

• $T=A_s \cdot f_y$

• $M_n = T \cdot (J_d) = A_s \cdot f_y \cdot (d-\frac{a}{2})$

• Verificar: $\varepsilon_s = \varepsilon_y$

3. Acero máximo y mínimo

3.1. Acero mínimo

En algunas situaciones el acero requerido por flexión es muy pequeño y es posible que la resistencia de diseño sea menor que el momento flector que causa el agritamiento en la sección ( $\phi M_n < M_{cr}$). Por lo tanto, el acero mínimo es para garantizar que el momento de la sección agrietada sea mayor que la no agrietada. Esto se debe a que si por alguna razón el acero instalado no es suficiente para llegar a una resistencia que causa el agrietameinto ( $M_{cr}$ ) y el momento externo lo supera, la falla será frágil y repentina.

Por tal motivo, la norma peruana E.060 requiere que el acero instalado garantice que $\phi M_n \geq 1.2 \cdot M_{cr}$. Para secciones rectangulares, esta condición se cumple con la siguiente ecuación:

$As_{min} = \frac{0.7 \cdot \sqrt{f'c}}{fy} \cdot b \cdot d$

3.2. Acero máximo

El acero máximo a instalar debe ser una fracción del acero balanceado. Esto es con el fin de garantizar una falla a tracción (sub reforzada). El acero máximo viene dado por la siguiente ecuación:

$As_{max} = 0.75 \cdot As_{bal}$

Donde, para secciones rectangulares el $As_{bal}$ se calcula como:

$As_{bal} = b \cdot d \cdot (0.85 \cdot \beta_1 \cdot fc / fy) \cdot \frac{\varepsilon_{c\mu}}{\varepsilon_{c\mu}+\frac{fy}{Es}}$

Bibliografía

• Ottazzi Pasino, G. A. (2011). Material de apoyo para la enseñanza de los cursos de diseño y comportamiento del concreto armado. (Tesis de maestría para optar el título de magister en ingeniería civil). Pontificia Universidad Católica del Perú, Lima, Perú. Recuperado de https://tesis.pucp.edu.pe/repositorio/handle/20.500.12404/1055